二項分布（確率論）について、簡単にご説明します。
ミニロトの抽選（31個の玉から5個引く）を6回して、同じ数字⑯の玉が2回出る確率は
Ｐ＝6Ｃ2×（5/31）＾2×（26/31）＾4
＾ｎとは累乗を表しており、（）内の数をｎ回かけ合わせます。
この答えはおよそ0.19（19％）です。このままでは使いづらいので、
31個の数字のうち6回抽選して、二回出る数はいくつあるのかという答えは、前の結果の31倍個となるので、およそ6個なります。
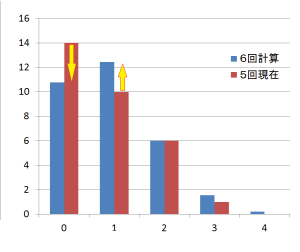
同じようにして、6回抽選して、一度も出ない数字はおよそ11個あり、一回出るのはおよそ12個あり、二回出るのはおよそ6個あり、三回以上出るのはおよそ2個となります。
このグラフでは5回現在、14個の数字が一度も出ていません。計算上6回抽選すると11個以下に減るはずなので、一度も出ていない数字から3個以上選ぶ必要があります。
私の場合は、6回と35回抽選でのこの二項分布を利用してます。
さらに一度も出ない数字だけに注目すると、19回抽選して一度も出ない数字は何個あるかという答えは、次の式で導きだせます。
Ｎ＝19Ｃ0×（5/31）＾0×（26/31）＾19×31
およそ1個となります。当たり前ですが、回数を増やせば増やすほど一度も出ない数字の個数は減っていきます。私は、この減り具合を表したグラフも利用しています。
基本的には、現在値が計算値（理論）より多ければ、そこから出ることになります。確定値というのは、厳密にいうと違うのですが、現在値（未確定）と合わせ鏡の数だと思ってください。
このように二項分布の形は常に維持されるように働きます。この分布を維持しようとする力を利用したのがベースＢです。ベースＢの中から数字が一つも出ないということは、今ある分布の形が大きく変形することを意味しています。
さらに、二項分布の形から大きく逸脱している箇所がある場合、そこには復元力（元に戻る力）が働くはずです。
以上のように、二項分布の維持力と復元力を利用して私は予想しています。
本来ならば、私が考案した予想の方法を公開するのはどうかなと思いましたが、そこまで記述してるサイトやブログも珍しいので、あえて公開しました。実際には計算値と実際の値がガッチリ合うことは珍しいです（10回に二回くらい）。しかし、計算値から大きく逸脱することの方がもっとまれなのです。
経験則については、その法則が破られることもあるし、説明がもっと長くなるので記述するのはやめておきます
この記事の無断転載・複製・転用は一切許可しません